이번 논문은 2017년 ICML에서 발표된 "Soft-DTW: a Differentiable Loss Function for Time-Series" 입니다. 이 논문은 시계열 데이터 간의 유사도를 측정할 때 가장 널리 쓰이는 기법 중 하나인 Dynamic Time Warping(DTW)이 미분 불가능하다는 단점을 극복하기 위해 기존의 DTW를 부드럽게(smoothly) 바꿔서 미분 가능하게 만든 Soft-DTW를 제안합니다. Soft-DTW는 시계열 간 유사도 측정을 딥러닝에 적용 가능하게 만들어, 다양한 응용 가능성을 열어주었습니다.
Soft-DTW: a Differentiable Loss Function for Time-Series
We propose in this paper a differentiable learning loss between time series, building upon the celebrated dynamic time warping (DTW) discrepancy. Unlike the Euclidean distance, DTW can compare time series of variable size and is robust to shifts or dilatat
arxiv.org
GitHub - mblondel/soft-dtw: Python implementation of soft-DTW.
Python implementation of soft-DTW. Contribute to mblondel/soft-dtw development by creating an account on GitHub.
github.com
🎯 DTW의 한계와 Soft-DTW의 제안

- DTW의 장점과 한계
- DTW는 cost 행렬에서 가장 비용이 낮은 하나의 정렬 경로 (alignment path) 만을 찾습니다.
- 위 그림에서 보라색 선이 최적 경로이고 이 경로만을 기준으로 두 시계열 간 거리를 계산합니다.
- 장점: DTW는 서로 길이가 다르거나, 시간 축에서 약간의 변형(늘어짐, 축소)이 있는 시계열도 유연하게 비교할 수 있습니다.
- 한계: DTW는 최적 경로 하나만 고려하며, 결과가 미분 불가능하여 경사하강법 기반 학습에 사용할 수 없습니다.
- DTW는 cost 행렬에서 가장 비용이 낮은 하나의 정렬 경로 (alignment path) 만을 찾습니다.
- Soft-DTW란?
- Soft-DTW는 "모든 가능한 정렬 경로"의 비용을 부드럽게 평균내는 방식입니다.
- 위 그림에서 보라색 외에도 주황색, 초록색 등 다양한 정렬 경로가 함께 고려됩니다.
- 이 평균을 계산할 때, soft-min 연산을 사용하여, 최적 경로 하나만 보는 대신 여러 경로를 고려하며 미분 가능성을 확보합니다.
- Soft-min 함수는 다음과 같은 수식으로 표현됩니다:
- $ \min_\gamma(a_1, a_2, ..., a_n) =
\begin{cases}
\min(a_1, ..., a_n), & \gamma=0 \\
-\gamma \log \sum_{i=1}^{n} e^{-a_i/\gamma}, & \gamma > 0
\end{cases} $
- $ \min_\gamma(a_1, a_2, ..., a_n) =
- Soft-DTW는 "모든 가능한 정렬 경로"의 비용을 부드럽게 평균내는 방식입니다.
🧠 Soft-DTW의 계산과 미분 방법
- Forward Pass: Soft-DTW 계산
- Soft-DTW는 DTW와 유사한 동적 계획법(DP) 방식으로 계산되지만, $(min, +)$ 연산을 $(-log-sum-exp, +)$ 형태로 대체합니다. 이로 인해 모든 경로의 soft-min 비용을 계산할 수 있습니다.

- Backward Pass: Gradient 계산
- 놀랍게도, Soft-DTW는 역전파(backpropagation)가 가능하도록 설계되어 있어, 손실값과 함께 gradient까지 얻을 수 있습니다. 이 덕분에 신경망의 학습 과정에 손실 함수로 통합할 수 있습니다.

📊 주요 실험 결과
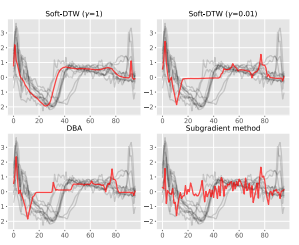
- 시계열 평균(Barycenter) 계산
- 기존의 DTW 평균 기법(DBA 등)보다 더 부드럽고 자연스러운 중심 시계열을 생성합니다.
- $γ$(스무딩 강도)를 적절히 조절하면 로컬 최소값에 빠지는 문제도 완화됩니다.
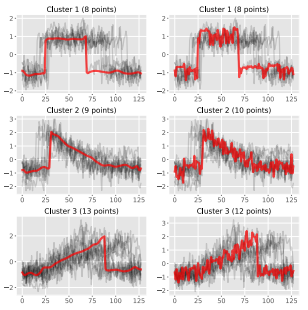
- 시계열 클러스터링
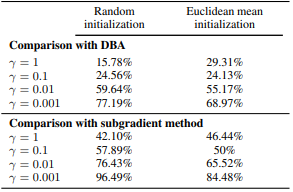
- Soft-DTW를 k-means에 통합한 경우, DBA보다 더 낮은 클러스터링 손실을 보여줍니다.
- 특히 $γ$ = 0.01 이하로 설정할 경우 성능이 가장 좋았습니다.
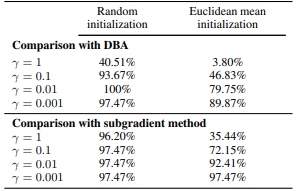
- 시계열 분류
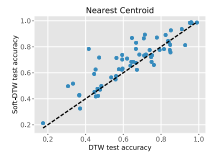
- Nearest centroid classifier에 Soft-DTW를 적용하면 DTW나 DBA보다 75% 이상의 데이터셋에서 더 높은 정확도를 기록했습니다.
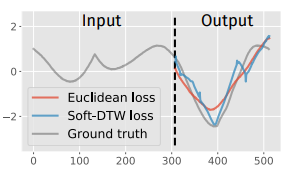
- 다단계 예측(Multi-step prediction)
- MLP 기반 시계열 예측에서, Euclidean 손실보다 Soft-DTW 손실이 더 날카로운 변화나 패턴을 잘 포착하는 것으로 나타났습니다.
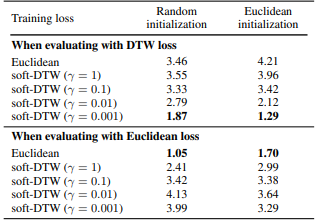
💡 Soft-DTW의 의의와 활용 가능성
- Soft-DTW는 단순한 거리 측정 기법이 아닌, 딥러닝 훈련에 직접 사용 가능한 손실 함수로 확장되었습니다. 특히 다음과 같은 분야에 응용될 수 있습니다.
- rPPG, ECG, 음성 등 시계열 기반 회귀 문제
- 시계열 생성을 포함한 Seq2Seq 구조
- 강건한 분류 및 군집화 모델 학습
📝 마무리
- Soft-DTW는 단순한 수치 기법을 넘어, 딥러닝 기반 시계열 분석의 가능성을 크게 넓혀주는 혁신적인 아이디어입니다.
- 시계열의 시간적 비선형성에 민감하지 않으면서도, 학습 가능한 손실 함수로 작동한다는 점에서 실용성과 이론적 기여가 모두 뛰어난 논문이라 할 수 있습니다.
'Deep Learning > Algorithm' 카테고리의 다른 글
| Prefix-Tuning: Optimizing Continuous Prompts for Generation (1) | 2025.05.23 |
|---|---|
| Parameter-Efficient Transfer Learning for NLP (0) | 2025.05.14 |
| LoRA: Low-Rank Adaptation of Large Language Models (0) | 2025.05.13 |