이번 논문은 2024년 NeurIPS에 발표된 "FactorizePhys: Matrix Factorization forMultidimensional Attention in Remote PhysiologicalSensing"입니다. 이 논문은 심박 신호 추정을 위한 다차원 Attention 계산을 Nonnegative Matrix Factorization (NMF) 기반으로 해결한 획기적인 구조인 FSAM을 제안합니다.
FactorizePhys: Matrix Factorization for Multidimensional Attention in Remote Physiological Sensing
Requests for name changes in the electronic proceedings will be accepted with no questions asked. However name changes may cause bibliographic tracking issues. Authors are asked to consider this carefully and discuss it with their co-authors prior to reque
proceedings.neurips.cc
GitHub - PhysiologicAILab/FactorizePhys: FactorizePhys: Matrix Factorization for Multidimensional Attention in Remote Physiologi
FactorizePhys: Matrix Factorization for Multidimensional Attention in Remote Physiological Sensing [NeurIPS 2024] - PhysiologicAILab/FactorizePhys
github.com
🎯 연구 배경
- 기존 rPPG 딥러닝 모델들은 attention을 아래처럼 분리하여 적용했습니다:
- 공간적 attention (이마, 볼 등)
- 시간적 attention (프레임 간 색 변화)
- 채널 attention (R, G, B)
- 이 방식은 간단하지만 세 차원 간 상호작용을 고려하지 못하고, 정보 손실이 발생합니다. 예를 들어, 이마에서 특정 채널의 특정 시간대 정보가 중요할 수 있는데 이를 통합적으로 표현하는 attention은 없었습니다.
- FactorizePhys는 NMF(Nonnegative Matrix Factorization)를 기반으로, 이 세 차원을 동시에 반영하는 다차원 attention을 계산합니다.
🧩 핵심 아이디어: FSAM (Factorized Self-Attention Module)
- CNN이 추출한 4차원 feature map:
- $\epsilon \in \mathbb{R}^{T \times C \times H \times W}$
- 시간($T$), 채널($C$), 공간($H \times W$) 차원 포함
- 이를 2D 행렬로 변환:
- $V \in \mathbb{R}^{M \times N}$
- 시간 차원을 $M$으로, 채널 및 공간을 $N$으로 압축
- NMF 수행:
- $V \sim WH$
- $W$: 기저 벡터, $H$: 계수 행렬

- 복원된 low-rank 행렬 $\hat{V}$ 를 다시 4D로 복원 → $\hat{\epsilon}$ → 이를 기존 feature $\epsilon$과 곱해 attention 적용
- Residual connection + instance normalization으로 안정화
🔑 주요 특징
- 기존 CBAM이나 SE-block처럼 채널별 attention만 학습하는 구조와 다름
- 공간-채널-시간 정보를 모두 보존한 상태에서 주목
- 추론 시 FSAM을 제거해도 성능 유지 → 학습 시 attention 효과만 유지 가능
🧠 구조 구성: FactorizePhys

- 입력: 원본 얼굴 영상 시퀀스
- Diff Layer: 프레임 차분 → 조명·배경 제거
- 3D Conv Layer + InstanceNorm
- FSAM 삽입 위치: 공간 크기가 7×7이 되는 위치
- 출력: 1D rPPG 파형 (심박 곡선)
🔧 FSAM의 범용성: EfficientPhys에도 적용

- 기존 EfficientPhys는 2D-CNN + TSM 기반
- SASN(Self-Attention Shifted Network) → FSAM으로 대체
- FSAM은 2D-CNN 구조에도 쉽게 통합 가능하며, SASN보다 일관된 성능 보여줌
📊 실험 결과 요약
- 데이터셋
- iBVP: 고정 조건에서 수집된 RGB+열 영상
- PURE: 다양한 움직임 포함
- UBFC-rPPG: 자연광 + 실내 조명
- SCAMPS: 고품질 synthetic 영상 (훈련 전용)
- HR 성능 (Cross-dataset 평균 MAE 기준 ↓)
- 전반적으로 FactorizePhys + FSAM이 최고의 성능을 달성함

- Ablation Study 요약
- FSAM의 효과: 기존 FactorizePhys에 FSAM 추가 시 MAE ↓
- Residual connection 유무 실험: 추가 시 성능 향상
- Rank=1인 low-rank factorization이 가장 좋은 성능
- FSAM 없이 추론해도 성능 유지 가능 → inference 최적화 가능
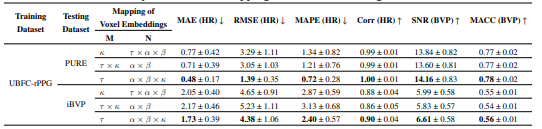
- 시각적 해석 (Visualization)
- Cosine similarity 시각화: FSAM이 적용된 모델에서 temporal 신호와 ground-truth 간 유사도가 높고, spatial 분포가 이마, 볼 등에 집중됨
- 실제 생리학적으로 타당한 위치에 attention이 집중

✅ 장점 요약
| 요소 | 내용 |
| 정확도 | 대부분 SOTA 모델을 능가하는 정밀도 달성 |
| 효율성 | 추론 시 FSAM 제거 가능 → 경량화 |
| 범용성 | 2D/3D CNN 구조 모두 적용 가능 |
| 해석 가능성 | attention 위치와 신호 성분이 직관적으로 시각화 가능 |
| 일반화 | 4개 공개 데이터셋 간 cross-dataset 테스트에서 강한 성능 |
📝 마무리
- FactorizePhys는 attention의 개념을 근본적으로 재정의한 rPPG 모델입니다.
- 기존처럼 채널/공간/시간 정보를 따로 처리하는 것이 아니라, 정보 손실 없이 통합적으로 처리할 수 있는 NMF 기반 attention 구조(FSAM)를 도입했으며, 이를 통해 심박 파형 추정의 정확도와 일반화 능력을 크게 향상시켰습니다.